I. INTRODUCTION
Image super-resolution (SR) is an important task in computer vision to increase or recover the size of a low-resolution (LR) image, generating a high-resolution (HR) output. This is usually referred to as single image super-resolution (SISR). SISR is an ill-posed problem, as there are various solutions for any LR image. Applications on SISR in recent years can be found in surveillance imaging [1], medical imaging [2], High-definition television, and more.
One of the traditional image upscaling methods involve the use of interpolation algorithms to increase image sizes. Thus, surrounding pixel data are utilized for generating the required additional pixel values.
Image super-resolution using Deep Convolutional Networks [3], also known as SRCNN was proposed by Dong et al to well tackle this problem and is the pioneer of deep learning-based SR study.
SRCNN [3] was performed in the HR space only by upscaling LR images before input via bicubic interpolation, but a Fast Super-Resolution Convolutional Neural Networks [4] (FSRCNN) was also proposed with transposed convolution to learn the upsampling process with the LR image as input. Additionally, an Efficient Sub-pixel Convolutional Neural Network (ESPCN) [5], which was proposed by Wenzhe Shi, efficiently generates HR images directly from the LR space and has been used by various algorithms as the standard upsampling module.
More complex and advance SISR algorithms successfully improve the performance in terms of PSNR (peak-to-signal-ratio). Namely, Enhanced Deep Residual Networks for Single Image Super-Resolution [6], and Residual Channel Attention Networks [7], usually known as EDSR and RCAN respectively. They prove the impact of network architecture on recovering image details for better performance. Attention mechanisms utilizing the channel and spatial attention are also key factors on SR performance in recent years. However, these algorithms do not only require heavy computation and huge amounts of parameters but are also able to upsample images by only a single scale factor with a single network.
More efficient lightweight SR networks like the Fast, Accurate, and Lightweight Super-Resolution with Neural Architecture Search [8], known as FALSR, use advance and more complex algorithms aiming at maintaining moderate performance while reducing the computational burden. Nevertheless, they aren’t able to upsample LR images by various scale factors with a single model.
Multi-scale Deep Super-Resolution [6], Cascading Residual Network [9], and Multi-path Residual Network [10] referred to as MDSR, CARN, and MPRNet respectively, are multi-path and multi-scale SR algorithms, which can output HR images of various sizes via a single model. They require separate pathways depending on the selected upscale factor and have outstanding results. However, each pathway has to be trained for a specific upscale factor, leaving out the rest, which can be considered a waste of parameters. In this paper, we propose a single-path upscale algorithm, utilizing all parameters of the model for every upscale factor. This reduces the network overall parameters while maintaining its performance.
The rest of the paper is organized in the following order. Section II gives reference to existing SR multi-scale learning algorithms. Section III shows an analysis of the problems in sub-pixel convolution for upsampling in SR and proposes a solution. Experimental results are shown in section IV, which leads to conclusions given in section V.
II. RELATED WORKS
In recent years, deep learning has been utilized for various computer vision tasks such as facial expression recognition [11], segmentation, etc. Dong et al were the first to use the deep learning convolutional neural network in SISR. The algorithm is known as SRCNN [3].
The SRCNN [3] network requires an upscaled image input to construct the desired HR image output. Bicubic interpolation is used to perform the input image preprocessing task not only in SRCNN [3], but also in models from algorithms including Very Deep Super-Resolution Networks [12] (VDSR), Deeply-Recursive Convolutional Network [13], and others. Therefore, the networks process images in the HR space only, which increases computation significantly and makes it impossible to analyze images in the LR space. Algorithms like the Efficient Multi-scale Super-Resolution [14], and, Balanced Two-Stage Super-Resolution [15] operate on images in both the LR and HR space for more accurate results.
Transpose convolution, also known as deconvolution, was proposed in FSRCNN [4] aiming at generating the HR output image in the last layer for efficiency and acceleration. This significantly reduced the computational burden and did not require bicubic input preprocessing. Improvement in performance with even fewer parameters compared to SRCNN [3] was also realized, concluding that operation on the LR space is essential in SISR.
ESPCN [5] proposed by Wenzhe Shi, introduced sub-pixel convolution for image upsampling, which also operates on images in the LR space.
Utilizing the sub-pixel convolution upsample module, huge and complex models like EDSR [6], and RCAN [7] offer outstanding performance. Algorithms that generate images visually pleasing to the human eye such as Super-Resolution using a Generative Adversarial Network [16], also use sub-pixel convolution to upsample images to the desired size. A similar technique known as sub-pixel mapping was implemented for text detection from video frames [17].
Unlike complex and huge computational models, FALSR [8] and CARN mobile [9] are lightweight models for efficient real-time implementation with a good performance-to-efficiency trade-off. They also utilize a learning-based upsampling technique.
Although learning-based upsampling methods are efficient and effective in terms of performance and efficiency, the limitation of these methods is that multi-scale learning is not possible. As first proven in VDSR [12], networks utilizing the interpolation-based upsampling method can train on images with various scales as the input image is upscaled before implementation. VDSR [12] proved better performance when trained with various scales. Compared to the methods training separate models for separate upscale factors, the advantage of VDSR [12] is that it trains a single model for multiple upscale factors, which saves parameters considerably.
Multi-scale multi-path learning or scale-specific multi-path learning is the process of learning for various scale factors with separate paths. This algorithm utilizes a single model efficiently for various scale factors. It is widely used in various methods such as MDSR [6], CARN [9], and MPRNet [10].
MDSR [6], which is an extension of the EDSR [6] model claim to realize a breakthrough in multi-scale training with sub-pixel convolution. They implement multi-path learning for the separate scale factor. FSRCNN [4] shows that after the whole model was trained for a certain scale factor, the whole model didn’t need training for the other scale factors. The performance obtained by training only the transpose convolutional layer for the other scale factors is the same as training the whole model for the other scale factors. This proves that shared parameters across various scale factors are present, which MDSR [6] use to their advantage.
MDSR [6] used multi-path learning for various scale factors. Multi-path learning in MDSR [6] consists of two elements. The first one is the preprocessing module for each scale factor separately, the second one is the sub-pixel upsample module for the separate scale factors. The central part of the network has shared parameters across all scale factors. During training, the central convolutional layers are trained for every scale factor, but each of the multi-path layers is trained for only one of the scale factors.
III. PROPOSED METHOD
We present a multi-scale single-path module exploiting the strong points of sub-pixel convolution and multi-scale training, and utilizing a single path for training. Our proposed method overcomes the need for multi-path learning and uses all the parameters for all upscale factors.
As first proposed in ESPCN [5], sub-pixel convolution is achieved by applying convolution to output a feature of s2×n channels. Then, pixel shuffling is applied by rearranging the pixels to increase the width and height of the feature by s while reducing the channel dimension to n. Therefore, channel dimensions are different for all scale factors. Note that s in s2×n represents the upscaling factor. As a result, MDSR [6] uses separate sub-pixel convolutional layers for different scale factors.
As shown in figure 1(a) MDSR [6] upsample module, the sub-pixel convolutional layer is used for each scale factor separately. MDSR [6] network use 64 filters for every layer, therefore, for scale factor ×2 in sub-pixel convolution, 22×64×64 filters are needed for the pixel shuffle upscaling process. Scale factor ×3 path layer needs 32×64×64 filters, which is reasonable. However, in the ×4 upscale layer, 42×64×64 filters cause a very huge number of parameters and therefore is replaced by doubling the scale factor ×2 upscale filter. Although it is an intuitive solution, it causes an imbalance in the number of parameters on the ×3 and ×4 upscale modules (32×64×64 > 22×64×64×2), which makes the ×3 upscale module possess the greatest number of parameters.
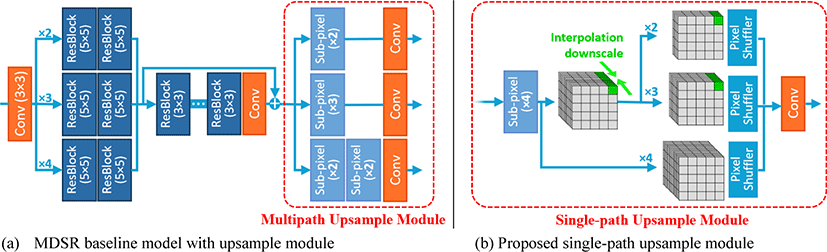
Another observed problem is that during training, each multi-path branch representing a certain scale factor will be trained one-third of the time compared to the central layers of the network. Moreover, when training for scale ×2 for example, ×3 and ×4 upscale layers are useless for the performance of the ×2 upscale layer.
We propose a solution as shown in figure 1(b). The green pixels shown in figure 1(b) are treated as the points to be downscaled via 1-dimensional interpolation. Note that the number of the green pixels represents the number of channels. Therefore, downscaling the pixels means reducing the number of channels. Thus, we reduce the channel dimension of the features from 42× n to s2× n when the required upscale factor is less than 4.
We firstly utilize the sub-pixel convolution for scale factor ×4 with 42×64×64 filters and use a 1-dimensional linear downscale on the channel axis of the feature map depending on the training scale factor. This reduces 42×64 channeled output to 22×64, and 32×64 channels for ×2 and ×3 scale factors while applying no reduction for ×4 factor upscale. Implementing sub-pixel convolution for scale factor ×4 allows the model to gather more parameters, and also lets the model perform channel compression for the ×2, and ×3 upscale factors. Thus, it exploits all its parameters for all the needed upscale factors. It can be formulated as:
where the low-resolution feature-map FLR, upsamples itself by an upsample function U. Wsc, Dli, and Sp represent sub-pixel convolution, linear downscale, and pixel shuffle upscale respectively.
With this solution, all parameters can be used across various scales without waste, which reduces the need for excessive parameters. As expressed in Table 1, the multi-path upscale branches require separate parameters for various scale factors. Consequently, compared to the single-path module, there are fewer parameters for each scale, and an imbalance in parameter numbers between scale factors ×3 and ×4 is observed. The single-path upscale module, on the other hand, uses all its parameters for all upscaling factors and is reduced compared to the total parameters of the multi-path upscale module. The parameters are reduced by 24% in the single-path module. More reduction can be identified when we also consider the last convolutional layers of the network shown in figure 1. This reduction is the same not only for MDSR [6] model but also for CARN [9] and MPRNet [10] as their multi-scale upsampling algorithms are the same as MDSR [6]. However, the lightweight mobile model from the CARN [9] paper called ‘CARN-M’ utilized group convolution in the upsample module, which makes it different from the MDSR [6] upsample algorithm. Nevertheless, parameters also reduce by 24% with the single-path algorithm.
| pscaling factor | Multi-path upsample module par. | Single-path upsample module par. |
|---|---|---|
| ×2 | 147.5K | 589.8K |
| ×3 | 331.8K | |
| ×4 | 294.9K | |
| Total | 774.1K | 589.8K |
IV. EXPERIMENTS
For a fair comparison, we train the MDSR [6] baseline model and train for the proposed algorithm by modifying the upsample module only. The same experiment is also performed for CARN-M [9] because its upsample module is composed of group convolutions with a group of 4. Although cubic interpolation is less memory efficient according to [18], we perform experiments on cubic downscale to compare their results with the multi-scale and linear downscale. Therefore, experiments are performed for multi-path, linear single-path, and cubic single-path using the MDSR [6] and CARN-M [9] models.
We employ the Div2K [19] RGB data images for training. Image data are cropped into 48×48 patches before training, and data augmentations include; flip and rotation to 90°, 180°, and 270°. The Set5 [20], Set14 [21], B100 [22], and Urban [23] datasets are used for evaluation and comparison.
We use a mini-batch of 16 and the L1 (Mean Absolute Error) loss also known as the MAE loss. Adaptive momentum optimizer [24] with a learning rate of 10-4 and halved at every 2×105 iteration updates. Xavier normal [25] is used as the weight initializer. The models are trained for 6×105 iterations. Although we trained the MDSR models almost exactly as presented in the EDSR-MDSR [6], paper, we didn’t implement the geometric self-ensemble procedure which was expressed as ‘MDSR+’. We utilize the same settings to train the CARN-M [9] model. For implementation, we utilize the PyTorch deep learning tool, with GPU RTX 2080.
As shown in Table 2, we compare results between multi-path, and linear single-path for MDSR [6]. We utilize the PSNR, structural similarity index (SSIM) [26], multi-scale structural similarity index (MSSSIM) [27], and universal quality index (UQI) [27] to show the achieved result. We only utilize the PSNR and SSIM to show the best and the second-best results. The linear single-path module performs better than the multi-path upsample module. It has a very similar performance to the cubic single-path results.
Shown in Table 3 are the results for the same experiments performed on the CARN-M [9] upsample module. The linear single-path and cubic single-path modules performed better than the multi-path module. However, the cubic single-path module performed slightly better than the linear single-path modules. Thus, the results show the effect the single-path modules have on sub-pixel convolution composed of group convolution.
Figure 2 (a) and (b) show the visual representation implemented with the MDSR [6] and CARN-M [9] model respectively. Due to its computational complexity, cubic single-path was expected to outperform other algorithms, but linear single-path algorithm performs better in terms of PSNR and SSIM in the case of MDSR [6]. It might be that when downscaling the features’ channels for pixel shuffling, utilizing cubic interpolation generates unnecessary values. This is because it implements a polynomial curve to fit four reference points. Linear interpolation utilizing just two reference points is enough. However, the output features generated from group convolution are generated from separate input features. That is the reason cubic interpolation works better on CARN-M [9] by using four reference points to downscale the features in the channel axis.

Although it increases the parameters, performance improvement can also be realized if we increase the number of channels of the feature to more than 42 × n before channel compression via interpolation downscale.
V. CONCLUSION
Through multi-scale multi-path SR analysis, we can identify the unshared and unbalanced parameter problems, formulate a solution by utilizing the advantages of interpolation algorithms, and exploiting sub-pixel convolution to its limit.
We can conclude that the linear single-path technique is a more practical solution compared to the multi-path algorithm because it reduces and exploits all its parameters for all scale factors. It also shows similar performance with less computation compared to the cubic single-path algorithm. The proposed technique can be applied to existing multi-scale multi-path SR models, such as MDSR [6] CARN [9], and MPRNet [10] even if they utilize group convolution.
Inspired by the results achieved from CARN-M [9], further research can be done by analyzing the group convolution in sub-pixel convolution to improve efficiency by reducing parameters and computation while maintaining good performance.












