I. INTRODUCTION
Within image segmentation techniques, thresholding methods are a simple and effective technique. Thresholding is commonly used to separate the object and background of an image and to distinguish important information in the image. Thresholding techniques do that the images are cut in two based on the selected threshold value in which greater intensities are classified as one and lower of that are into other. Although many segmentation methods are developed to segment the object of the image, thresholding techniques are very low computational cost compared with other methods. As mentioned, the thresholding idea is obvious, but the problems are the selection of threshold values. The threshold selection methods are mainly based on a histogram of images, and the techniques are suggested in many research works [1-3]. There are many thresholding techniques such as histogram shape-based, cluster-based, entropy-based, spatial-based, network-based, etc [4-5]. In this work, we suggest the refined histogram extension for popular cluster-based methods to order to reduce big bin problems.
Generally, the thresholding techniques are divided into two main groups: global and local thresholding. Global thresholding uses the histogram of the whole image to select the threshold value. In local thresholding, images are separated by different regions and they are independently selected by the threshold values in those regions [6].
If the histogram has some large bins which occupy the most density of whole intensity distribution, it is a problem for global thresholding methods. We refined the histogram to overcome the big bin problem in which sub-bins are created from big-bins based on distinction metric [7]. Median-based and Otsu thresholding methods are used in our work, and those thresholding methods [8-9] are common techniques. In order to define the threshold value in Otsu thresholding, intra-class variances are calculated for every possible deal, and then the threshold value is determined at minimum intra-class variance. If the histogram of an image has two peaks relating to objects and background, the Otsu thresholding result is much better than others. However, if two peaks of the histogram have some big bins, there is still a problem in selecting the optimal threshold value. Our experimental results show that they work more effectively on the refined histograms.
Our work is organized in the following sections, and thresholding basics are discussed in section II. The refined histogram is described in section III, and Section IV shows some results implemented on original and modified histograms. Our conclusions are in Section V.
II. THRESHOLDING TECHNIQUES
Assume that an image f(x, y) has M×N pixels and an intensity range is 0 < f(x, y) ≤ 255, x ∈ [0, M-1], and y ∈ [0, N-1]. A threshold t is used for images into two classes:
The histogram intensity levels of the image f (x,y) are (i note 0 < i ≤ L-1), and the histogram denotes h(i).
The idea of Otsu thresholding is to find an optimal threshold value based on minimizing intra-class variance which is calculated for every possible threshold value.
Variances of two classes are noted by σ2bg and σ2fg, and defined by:
where, Nbg and Nfg are numbers of the pixels, and ubg and ufg are means of two classes, respectively. Means are calculated by:
Intra-class variance is computed by
where wbg and wfg are the weight of two classes and computed by:
To find the optimal threshold value, the Otsu algorithm is expressed by that we do the following steps for each threshold value, iteratively (step 1 to step 4):
-
Divide into two classes based on the threshold value t.
-
Calculate the weights of each class (equation 5).
-
Estimate the means of each class (equation 3).
-
Compute the intra-class variance of two classes (equation 4).
-
Select the optimal threshold based on minimizing intra-class variances.
III. REFINED HISTOGRAM
In order to provide neighborhoods of all pixels of f(x, y), let g(x, y) be the extended image that is surrounded m times by zero intensities:
We proposed the distinction metric in our previous work [8] and the distinction metric is computed by the cumulative difference between current pixel intensity and its neighboring pixel’s intensities. It is expressed by the following formula:
where D is the distinction metric computed by equation (7) and Rm(x, y) is a local square in the m by m square neighborhood centered on f(x, y).
Based on the distinction metric, we can divide one big bin into many sub-bins. For instance, in Fig. 1, we can see that the intensity (i=30) of the image occurs in high density in its histogram. However, they may have different neighbors. Fig. 1 shows the demonstration of the big bin dividing into the sub-bins process.
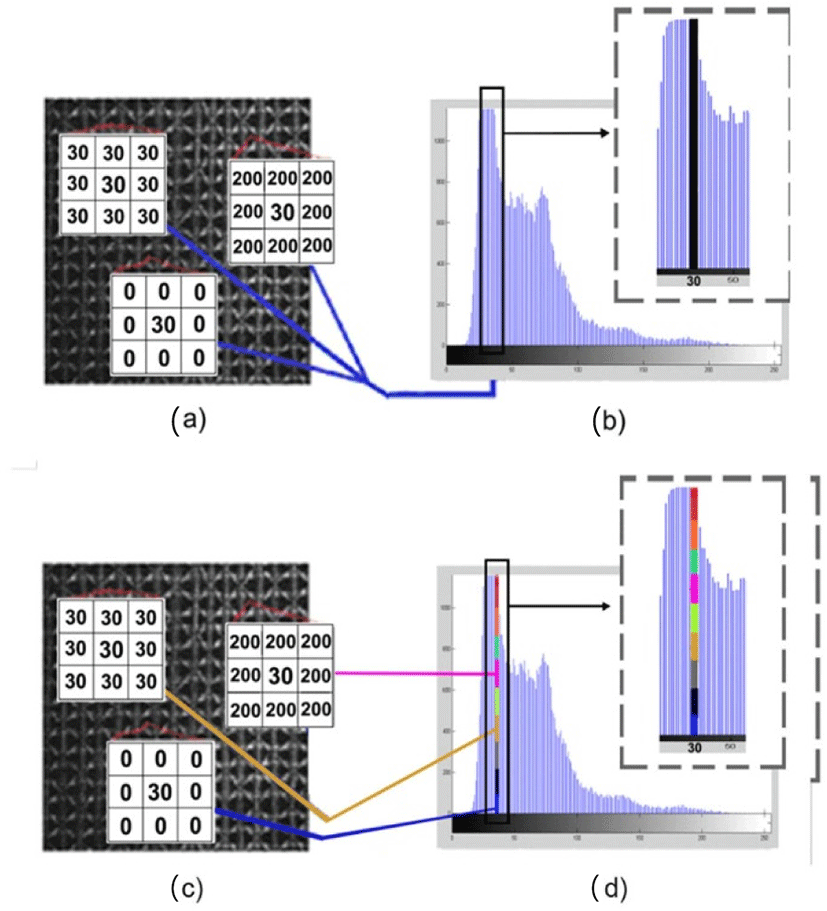
IV. EXPERIMENTAL RESULTS
This work aimed to show that one thresholding method gives different results when tested on the original and the refined histograms. In the experimental, we used six images: two images are chosen from the Brodatz texture dataset [10], both of them are selected from DIBCO (2019) datasets [11], and others are used [12]. All selected image histograms have some big bins in which the densities of the histogram are high. Otsu and median threshold selections are used for segmenting foreground from background in those images for comparison.
In order to evaluate effectiveness, we use intersection over union (IoU) criteria, and it is expressed by the following:
where, A is the resulting image and B is the correctly binarized image (ground truth).
The experimental results show that the segmentation result used in the refined histogram is much better than that of the original. In Table 1, we can see more detailed pieces of information on the comparison.
In Table. 1, we can see histogram bin sizes and temporary bin sizes of refined histograms in the Bin number rows. Threshold (T=) row shows selected thresholding values of the original and refined histograms for each method, respectively. IoU row is their values of evaluation metric.
Fig. 2 shows the results of median thresholding on two test images in track A of the DIBCO-2019 dataset, and their ground truth mask images are shown in Fig. 2(c) and (d). In Fig. 2(e) and (f) result images are tested on the original histograms, and (h) and (i) result images are tested on the refined histograms. In Fig. 2(e), the texts are not clearly shown while the texts are clearly shown in (h). By contrast, background texts are more segmented with proposed texts on the original histogram in Fig. 2(f), and it was reduced on the refined histogram in Fig. 2(i).

In Fig. 3, two sample images (D34&D42) of the Brodatz dataset are thresholded by the Otsu method on their original and refined histograms. The images are in Fig. 3(a) and (b) and its ground truth masks are illustrated in Fig. 3(c) and (d).

Fig. 3(e) and (f) show the results of original histograms, and the mesh shown (e) has not clearly segmented compared to the refined histogram in Fig. 3(h). Similarly, Fig. 3 (i) shows the result of the refined histogram and it is better than the original one.
In Fig. 4, the Otsu and Median methods are used for segmenting, and their result and ground truth mask images are shown in Fig. 3(a)-(i), respectively. In Fig .4(e) and (f), both segmented results on original histograms are shown, and Fig. 4(h) and (i) are results of the refined histograms. The fishtail in Fig. 4(h) is the result of Otsu thresholding and it is better segmented in the refined histogram for comparison with the result of the original histogram Fig. 4(e). The screwdriver shown on the right bottom of Fig. 4 (i) is the result of the median-based and it is also better segmented than that of the original histogram Fig. 4 (f).

Our experimental results prove that the results of them on the refined histograms are more effective compared with the original ones.
V. CONCLUSION
We suggest the refined histogram for preprocessing of thresholding in order to reduce the big bin problem. In the work, we use Otsu and median-based thresholding techniques and six test images are chosen from DIBCO (2019) track A, Brodatz dataset, and others.
In order to reduce big-bin problem, we refined the histogram of the image using neighborhood distinction metric. Our experimental results prove that their results on the refined histograms are more effective compared with the original ones.
Further work will be to compare different thresholding methods’ results on a refined histogram using different neighborhood metrics.










