I. INTRODUCTION
Massive amounts of information, particularly employment records from earlier periods, are sitting idle in undergraduates’ management information systems. It is imperative to integrate educational management resources at all levels and to provide a scientific basis for macro decision-making. Employment rate and quality of college graduates can be improved through the analysis of prior employment data, the mining of the major variables influencing employment, and the provision of decision assistance for decision-makers [1-3]. The primary purpose of analyzing employment data is to discover some basic patterns and hidden knowledge behind the data [4-5]. The decision tree classification technique, which is extensively used in data mining, has recently been suggested as a solution to this challenge by a number of academics [6-7].
Based on machine learning algorithms, it is reasonable and feasible to analyze the employment destinations and methods through the employment data of undergraduates [8-10]. Applying machine learning algorithms to predict employment conditions and directions has opened up a new space for improving higher education. While deep learning has gained popularity recently, decision tree algorithms are still widely used in various fields, including data mining, machine learning, and artificial intelligence. Decision trees are particularly suitable for analyzing data with discrete and categorical variables, which is the case for the study. In addition, decision trees are easy to interpret, and the resulting rules can provide valuable decision support for decision-makers. Moreover, the study aims to analyze the employment situation of innovative talents based on artificial intelligence. Deep learning has shown impressive performance in various applications, but it may not be the best choice for our specific research question. While deep learning algorithms are often used for tasks such as image recognition, natural language processing, and speech recognition, which typically require large amounts of data and complex features. Therefore, a decision tree algorithm based on a multi-scale rough set model is a suitable choice for the study, as it can effectively handle the complexity and noise in the dataset while providing easy-to-interpret rules for decision-making. According to different colleges, the students taught by high-level universities have more vital learning abilities, more academic levels, and more opportunities than students from unknown schools. Therefore, the probability of direct employment will be lower than for undergraduates from unknown colleges. The employment environment of students when they graduate will directly affect the employment of undergraduates [11]. More students choose to continue their studies when the economic situation could be better when they graduate. For example, during COVID-19, more undergraduates choose to take the postgraduate entrance examination; When the economic situation improves, more students will choose employment directly [12].
The employment data in colleges is dynamic and complex. If we conduct data analysis simply, we may be unable to explore the issue's essence and reality. Conventional algorithms are sufficient for mechanical work, but the data provided by the analysis needs to provide a valuable reference for college education. Machine learning is algorithm research that can be automatically improved through the continuous accumulation of experience [13]. Therefore, it is very suitable for research on employment data in colleges. Machine learning can use the data of specific college employment situations to continuously optimize the algorithm and analyze and view the situation of employment and college education from a dynamic perspective. The analysis and conclusions drawn are more reasonable and informative.
The overall employment situation of undergraduates is becoming increasingly severe. Simultaneously, the rapid development of new media technology has significantly impacted people's life, study, employment, and other aspects [14]. The question of how students and society at large can best leverage on the potential benefits of new media to boost the employment prospects of undergraduates is a subject of widespread interest and debate. New media is a form of communication that relies on the Internet to provide users with information and services. Combined with personal mobile terminals, the network provides information services to the public through computers, mobile phones, pads, and other carriers, promoting the formation of the new media era. The characteristics of openness, interactivity, and immediacy of new media have brought convenience to information exchange, significantly improved the richness and diversity of information resources, and simultaneously impacted all aspects of people's lives [15]. Most strikingly, new media has built a smooth and high-speed bridge between employers and undergraduates, enabling efficient information transfer between various enterprises and undergraduates and significantly improving the employment success rate of undergraduates. The influx of massive data in the new media makes it possible for undergraduates to be confused by information that is difficult to distinguish between true and false [16-17]. Therefore, it is necessary to analyze the employment situation of innovative talents based on artificial intelligence.
Historical employment data are typically noisy data due to the variety and intricacy of real employment circumstances, and there is considerable variation among organizations with respect to the precision with which decisions must be made. In earlier times, there was no better way to deal with issues like conflicting demands for decision-making precision and noise flexibility [18-19]. However, by bringing the multi-scale idea into the rough set theory via the idea of a variable-precision rough set, the multiple scale rough set model-based method can effectively address this issue. Thus, the main contribution of this study is the multiple scale rough set model-based decision tree (MSRS-DT) is proposed for analyzing employment outcomes for college graduates.
The remainder of this paper is organized as follows. Section 2 presents related studies on data classification and rough set. Section 3 uses MSRS-DT to analyze the employment data of colleges. Subsequently, Section 4 presents the experimental results and analyses. Finally, Section 5 concludes the paper.
II. RELATED WORK
Data mining is a hot issue in database knowledge discovery research, generally the automatic search and extraction of previously unknown and potentially available patterns through algorithms from a large amount of collected data [20]. Information and communications technology has opened up all links of data transmission. Information and communications technology has broken through all data transmission links, generating massive data. Large-scale data mining involves searching for complex patterns under TB or even EB-level data [21]. The classification problem has always been a research hotspot in data mining. In data mining, data models can be obtained by classifying data tuples. Once the data classification model is obtained, it can be used to predict and classify data to give people a better understanding of data. However, computational efficiency and scalability have become the two most severe challenges data mining faces, and only a few classification methods can be applied to data analysis [22].
Some deep learning approaches are provided for classification [23-26]. Many classification methods are based on statistics and machine learning, among which the decision tree classification algorithm is the most widely used. The decision tree is a classification algorithm based on inductive learning, which mainly includes two stages: construction and pruning [27]. A decision tree is built using a top-down, iterative, divide and conquer methodology [28]. The critical steps in creating a decision tree from a decision table are selecting branch attributes and dividing sample sets. The decision tree classification algorithm has attracted much attention among various data classification algorithms due to its fast construction speed, apparent structure, and high classification accuracy. In [29], Bian and Wang proposed a novel college-enterprise cooperation mechanism divided into three parts. In [30], the authors presented a hybrid classifier system that used clustering to improve the accuracy of the decision tree. In [31], the authors provided a method for enhancing machine learning decision trees' accuracy-interpretability trade-off. In [32], the authors used confusion matrix to optimize decision tree. To address the poor interpretability of the results generated by conventional fuzzy clustering algorithms, in [33], the authors built an unsupervised multi-way fuzzy decision tree, in which each cluster is made up of one or multiple pathways. In [34], the authors presented a fuzzy frequency algorithm of preordered capacity of node linked list for mining fuzzy association rules. This algorithm accelerated the building of trees and the speed of locating frequent fuzzy item sets.
Rough set theory is a mathematical tool proposed by Pawlak to deal with fuzzy and uncertain knowledge [35]. It has been successfully applied in machine learning, smart system, decision analysis, knowledge discovery, and data mining [36-38]. The Pawlak rough set model cannot adapt to the complex system processing mechanism and noisy data. To enhance the anti-interference ability of the rough set model, Ziarko proposed variable precision rough sets that introduced β (0≤β<0.5) based on the Pawlak rough set model [39]. It allows a specific misclassification rate and later defines β as the correct classification rate (0.5<β≤1). In [40], the authors presented a brand-new classification method based on skewed decision trees with fuzzy rules.
III. METHODOLOGY
The method for generating decision tree employing the multi-scale rough set model is grounded in the theory of variable precision rough set. It takes into account the characteristics of the scaling factors, and presents the various decision criteria at various levels of the decision tree.
Assuming that scaling function φ(t) ∈ [0.5,1.0], (t = 1,2,⋯, N). We have
The classification characteristic at each node must be chosen before a multi-scale rough set decision tree can be constructed. The most reliable evidence for a decision rule can be obtained. To determine the range of this approximate classification, we use the multi-scale rough set to describe the approximate classification accuracy dci(D) [41]. As the value of the approximate classification characteristic increases, decision analysts will have access to more factual information as well as potential functional variables. More nuanced details and potentially relevant uncertain details can be given for decision analysis if the estimated classification attribute's value is increased.
Let multi-scale decision information system be S = (U, C ∪ D, V, φ(t)), where U is the global domain, C is the conditional attribute set, D is the decision attribute set, φ(t) is the decision function, Ci is the conditional attribute of C. {X1, X2, ⋯, Xn} is a subdomain of Ci in global domain U, {Y1, Y2, ⋯, Yn} is a subdomain of the decision attribute D in the global domain U.
Here, we describe the precision of an approximate classification as follows.
where is the φ(t) lower approximation of Yi, and . is the φ(t) upper approximation of Yi, and .
Given the inhibitory factor: regarding the decision table information system, S = (U, C, D, V, φ), C and D are called condition attribute set and decision attribute set respectively. U/C = {x1, x2, ⋯, xn}, U/D = {y1, y2, ⋯, ym}, and the decision rule is rij : des(xi) ⇒ des(yi).
Assuming kij is the possibility factor of decision rule rij, kij = |xi ∩ yi|/|xi|, and 0 ≤ kij ≤ 1. Where |xi ∩ yi| is the whole sample numbers that meets the decision rule xi → yi, and |xi| is the number of samples meeting the antecedents of the decision rule.
Let , where yij is the inhibitory factor of the object set of a certain condition attribute on the decision attribute, referred to as the inhibitory factor. The value of the decision attribute corresponding to the inhibitory factor yij is recorded as D0.
From the definition of the inhibitory factor, if the inhibitory factor of the global domain U is more significant than a given threshold λ(0 < λ ≤ 1), it means that at least % instances of a decision rule go to the value des take the same value D0 on the decision attribute. In this case, the condition attribute value φ(a, Xi) is retained, and generating the decision tree down is no longer necessary. The leaves are directly marked with D0 to mask the adverse effects caused by a few noise data on the decision tree.
In light of the foregoing, a multi-scale rough set model-based decision tree generation method can be derived.
Input: multi-scale decision information system S=(U, C ∪ D, V, φ(t)), global domain U, conditional attribute set C, decision attribute set D, decision function φ(t), threshold λ (λ > 105).
Output: a decision tree.
Step 1: Generate a node N.
Step 2: Calculate the approximate classification accuracy dci(D) of each conditional attribute C corresponding to D concerning φ(t). The value with the smallest corresponding equivalence class is selected if there is the same dci(D) value.
Step 3: If dci(D) ≥ φ(t), go to Step 4. Otherwise, go to Step 6.
Step 4: Calculate the value of the possibility factor kij and the inhibition factor yci(Xi) corresponding to the current conditional attribute C, and go to Step 5.
Step 5: According to the calculated inhibitory factor yci(Xi) value compared with the threshold λ, if yci(Xi) ≥ λ, the current condition attribute value φ(a, Xi) was retained to mark the leaf nodes with D0, and the calculation of this subset was finished. If yci(Xi) < λ, then select the subset divided when the condition attribute value is φ(a, Xi) as the new object set, and return to Step 2.
Step 6: According to the selected condition attribute node, the object set is divided into several subsets, and the decision attribute value corresponding to the subset is calculated. If the attribute values are the same, the leaf nodes are directly marked with the decision attribute values, and the calculation of the subset is terminated until all subsets are finished. Otherwise, these subsets are selected as the new object set, and Step 2 is returned. Overall, the framework for the methodology is plotted in Fig. 1.
IV. EXPERIMENT AND RESULTS ANALYSIS
To effectively collect and evaluate employment data, we need a clear subject of data analysis. Graduates from Changchun University of Technology in 2021 provided the data for this analysis. The attributes related to employment are extracted, such as gender, major performance, English level, computer level, technological competence, and employment unit. According to Table 1, 20 examples are taken as the employment training sample set, the condition attribute set is C = {e1, e2, e3, e4}, and the decision attribute is D = (d).
Note: e1 Major performance: Excellent (3: average score>90); Good (2: average score in 75−90); Average (1: average score<75). e2 English level: none (1: no certificate); CET-4 (2: pass the College English Test band four); CET-6 (3: pass the College English Test band six). e3 Computer level: RL (1: relatively low computer level); RH (2: relatively high computer level). e4 Technological competence: Junior (1); intermediate (2); senior (3).
According to the unit structure of the undergraduate's employment unit d, the employment unit is classified as government agency (A), privately held company (B), and foreign-funded enterprises (C). State-owned companies, and universities are all examples of government agencies. Businesses run by private or groups are often referred to as "private enterprises." Joint ventures between Chinese and international companies are also considered to be foreign-funded businesses. They are divided into echelon groups according to the benefits and geographical location provided by various types of enterprises. The quantified values are excellent public institutions (A1), ordinary public institutions (A2), excellent private enterprises (B1), ordinary private enterprises (B2), excellent foreign-funded enterprises (C1), ordinary foreign-funded enterprises (C2).
Using the above multi-scale rough set as a basis, we generate a decision tree with scaling function of φ(t) = 0.6 and a threshold of 0.8. The following steps outline how to build a decision tree.
-
(1) By using the equation (2), compute de1(D)=0.74, de2(D)=0.15, de3(D)=0.32, and de4(D)=0.32.
-
(2) Select the attribute e1 as instructed in Step 2 of the presented method. In other words, the node e1 represents the major performance.
-
(3) Since de1(D)=0.74≥0.6, go to Step 4 of the pro-posed algorithm.
-
(4) There are three possible values (1, 2, 3) for the attribute e1. The generated tree displays three distinct branches. Attribute e1 is considered a leaf when the inhibitory factor is less than one and e1 = 1. If yci(Xi) < λ, as in the instances of e1 = 2 and e1 = 3, then the computation of Step 2 is repeated.
-
(5) Once more, using equation (2) to estimate the approximate value, we obtain a maximum of de4. Hence, pick the node whose property is tree. The generated decision tree is shown in Fig. 2.
Depending on the scaling function used, the decision tree generating method may generate decision trees with a variety of sizes. Therefore, we set φ(t) = 0.8 for calculation and analysis, respectively. The above computation yields a decision tree with ten nodes, three levels of depth, and some six-leaf nodes, as depicted in Fig. 3.
According to this study's analysis of experimental findings, the prominence of the scaling function, the level of precision in the representation of knowledge, and the total number of decision rules all rise with the value of the scaling variable. The generated decision tree structure, however, is also more complicated. This is due to as the number of scaling factors increases, the decision tree generation method for the multi-scale rough set model will produce a narrower range of estimated bounds matching to the decision characteristics, and a wider collection of decision rules. It should be observed that as noise rises, the scope of decision rules also grows, and that the certainty of some of the rules acquired may fluctuate. As a result, it is crucial to carefully weigh the needs of various audiences in terms of the precision with which decisions can be made. The decision analysis dataset and the precision of the user's research queries should inform the choice of the scaling function's values, which should then be chosen sensibly.
Rule 1: Major performance = 'medium': ordinary private companies.
Rule 2: Major performance = 'good' & technological competence = 'intermediate': ordinary private companies.
Rule 3: Major performance = 'good' & technological competence = 'senior': ordinary public institutions.
Rule 4: Major performance = 'excellent' & technological competence = 'intermediate': excellent private companies.
Rule 5: Major performance = 'excellent' & technological competence = 'senior': excellent public institutions.
When φ(t)=0.8, it is also possible to derive the decision rules for the decision function from Fig. 2, and these rules will not be listed in depth here.
It is imperative to augment the professional caliber of students through innovative talent training programs. Additionally, the design of professional courses should closely align with practical work settings. For private enterprises and public institutions, where the employment direction of graduates is mainly concentrated, students should obtain more advanced skill certificates, especially grade certifycates that public institutions recognize more.
The experimental training set, presented in Table 1, is utilized as the employment data to assess the efficacy of MSRS-DT for employment data mining. The algorithm under consideration is evaluated against C4.5, rough set, secure decision tree classification (SDTC) scheme, and artificial bee colony and gradient boosting decision tree algorithm (ABCoDT) [42-45]. Table 2 displays the utilization of the proposed algorithm for the examination of employment data. Although the generated rules are relatively simple and the tree structure has limited scale and depth, there exist datasets that cannot be separated.
| Method | Scale | Depth | Number of rules |
|---|---|---|---|
| C4.5 | 24 | 6 | 9 |
| Rough Set | 16 | 5 | 11 |
| SDTC | 42 | 4 | 7 |
| ABCoDT | 10 | 3 | 6 |
| The proposed (φ(t) = 0.6) | 8 | 3 | 5 |
| The proposed (φ(t) = 0.8) | 10 | 3 | 6 |
Both the depth and precision of the assessment decision tree's classification are crucial. According to the classification finding model, complexity is measured by how easy or difficult it is to describe the issue using the rules of the model. The quality of a classification algorithm is measured by how well it can forecast previously unknown data classes. When handling large amounts of data, higher precision in classification implies better results.
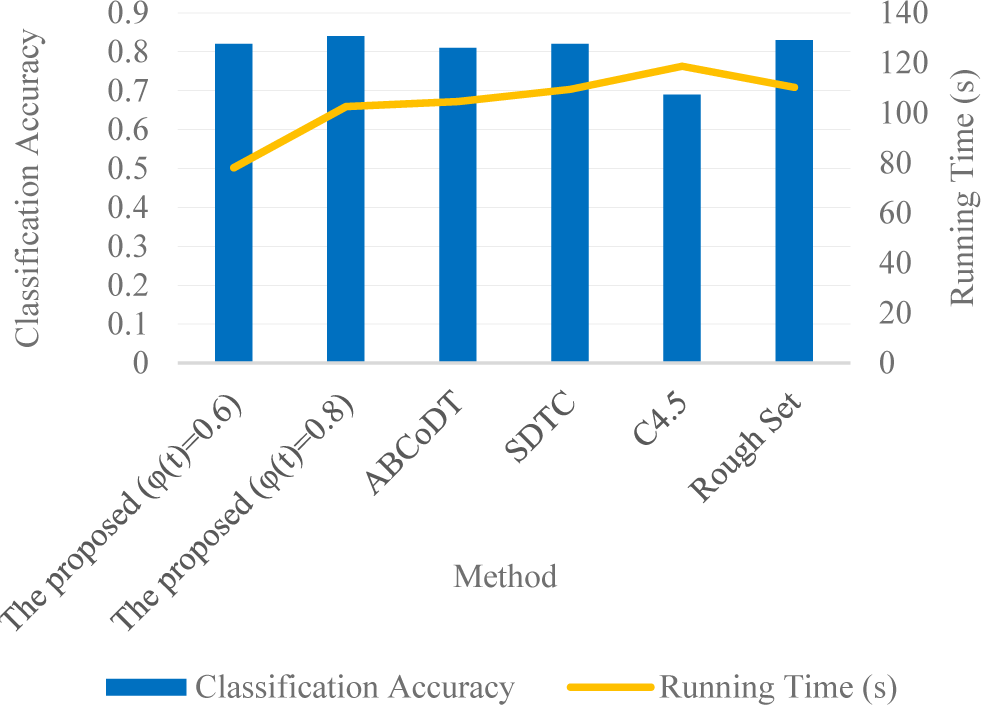
The experiment selected 1,000 employment records as the test set and runs a test experiment on the decision tree model established with the training data. The classification accuracy and running time of this method were compared to baselines. Fig. 4 displays the outcome of the study analysis. According to the findings, the MSRS-DT has a better performance than that of baselines. Under varying scaling function values, its classification accuracy is inferior to that of the baselines, but it outperforms baselines in terms of processing speed.
From the data analysis of the employment situation in colleges, many other factors can affect the employment situation of undergraduates, such as gender ratio, hobbies, and market demand. The discussion of the information provided by big data should comprehensively analyze the factors that significantly impact the employment of undergraduates rather than only consider the employment choice data of undergraduates. As long as the algorithm ability of machine learning is fully utilized, the problem of low objectivity and accuracy of information collection in existing research can be effectively solved. Additionally, it can help students make more informed decisions about their academic and career paths. For example, if the analysis identifies specific skills or qualifications in high demand among employers in the new media industry, students could be encouraged to pursue courses or internships that develop those specific skills. Alternatively, if the analysis suggests that certain jobs are becoming automated or less in demand, students could be advised to consider alternative career paths. Another potential application could be to help educators design curricula that better prepare students for the job market. For example, if the analysis shows that employers place a higher value on skills such as data analysis or social media management, educators could incorporate more coursework or projects to develop those skills.
V. CONCLUSION
Currently, the employment situation is becoming increasingly severe. Colleges should increase the integration of resources, improve the intensity of scientific decision-making, and rely on scientific means to effectively improve graduates' employment rate and employment quality. The MSRS-DT algorithm is proposed for improving the employment rate. To ensure that the produced decision tree can accommodate a variety of users' requirements for decision precision, it employs the inhibiting factor to perform a preliminary round of pruning.
Based on the optimization and progress of the machine learning algorithm, the data analysis on the employment situation of colleges will help to comprehensively and objectively analyze the specific employment situation of undergraduates and provide a good reference for colleges to predict the graduation trend of graduates in advance. Since machine learning algorithms are not a paradigmatic, fixed analysis method and research approach, machine learning algorithms should be able to appropriately add more variables and factors in the practice and application of higher education and employment in the future, and it can better assist in enhancing employment services in colleges and improving education levels.